Introduction to Data Science: A Comp-Math-Stat Approach

1MS041, 2021

©2021 Raazesh Sainudiin, Benny Avelin. Attribution 4.0 International (CC BY 4.0)

14. Supervised Learning & what is machine learning?

Topics

Let’s start by talking about a few examples of supervised learning problems. Suppose we have a dataset giving the living areas and prices of 47 houses from Portland, Oregon:

In the case of simple linear regression we could set $x$ to be the size in square feet and $y$ to be the price, the goal would then be to find a function $f(x)$ that is close to $y$ in some sense.

In the context of machine learning they often use the following terminology: let $x^{(i)}$ denote the features(living area) and let $y^{(i)}$ denote the target (price), then a pair $(x^{(i)},y^{(i)}$ would be called a training example.

In this terminology they also call the set of observations $\{(x^{(i)},y^{(i)}),\, i=1,\ldots,m\}$ a training set.

In this context the goal is statistical prediction

Contrast this with the statistical estimation viewpoint of linear regression, where the goal is to estimate the parameters.

Why is this difference, basically it is one of explainability. Estimation is often used as a tool to explain something through its statistical model and the estimated parameters of the model. Lets assume that there is a linear relationship between fat percentage and BMI, but we do not know the parameters. Then by simply taking a few observations and performing a parameter estimation under a given loss, such as the maximum likelihood estimator (MLE), we can do hypothesis tests to check if the parameters are positive or test between different proposed values of said parameters. The goal in statistical machine learning is often one of prediction, and as you will see, the models that are often in use, do not allow us to actually explain anything, although the prediction is also accomplished by first estimating parameters of a model but with the explicit goal of predicting future from past observations.

In conclusion, in statistical machine learning we are often using weaker model assumptions, but since we are focusing on prediction we do not really have a problem. In contrast, in classical statistical decision problems, the focus is on stronger model assumptions and the goal is to extract more detailed information about the relationships between features and targets to obtain a better explainable understanding of the underlying data generating process.

Think of the name, machine learning. From this you get that the focus has to be the behavior of the machine (prediction).

It is important to bear in mind that estimation for explainability and estimation for predictability are both formally statistical decision problems. Here, we take such a mathematical approach.

Supervised learning

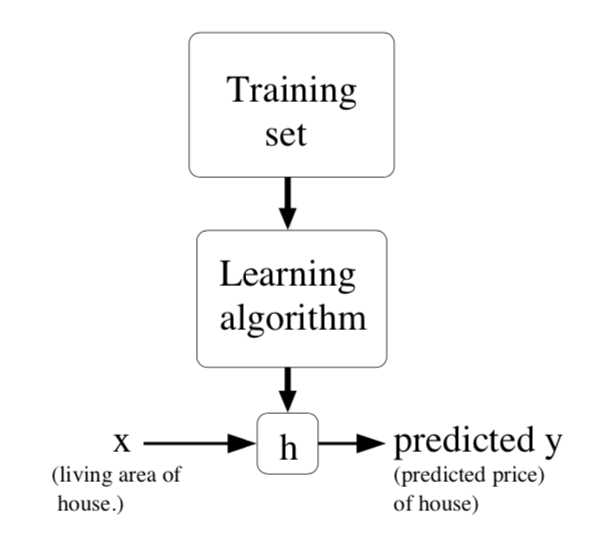
The schematic overview of supervised learning is the picture below

What we will cover in this and coming lectures

Probabilistic viewpoint of machine learning

To describe the supervised learning problem slightly more formally, our goal is, given a training set, to learn a function $h : \mathcal{X} \to \mathcal{Y}$ so that $h(x)$ is a “good” predictor for the corresponding value of $y$. For historical reasons, this function h is called a hypothesis in the machine learning community and should not be confused with hypothesis testing from classical statistical community. The class of all functions that we are searching in is called the hypothesis class in this nomenclature (denoted $\mathcal{H}$).

The process of learning can for many supervised algorithms be written as follows: $$ \arg\min_{h \in \mathcal{H}} \sum_{i=1}^m L(h(x^{(i)}),y^{(i)}) $$ where $L$ is a so called loss function or cost function, we will see how this loss function in most cases is the log-Likelihood for some underlying model. In order to describe this process we need to dig a bit deeper into the concept of regression:

In the case of linear regression we assumed that the regression function $r(x)$ $$ r(x) = E(Y | X=x) = \int y \, f(y|x) dy $$ was linear, i.e. $r(x) = \beta_0 + \beta_1 x$, furthermore we assumed that $$ V(Y | X=x)=\sigma^2, \quad \text{independent of $X$} $$ We assumed that $$ \boxed{\displaystyle{\epsilon_i | X_i \sim Normal(0,\sigma^2) \quad \text{ i.e., }\quad Y_i|X_i \sim Normal(\mu_i,\sigma^2), \quad \text{ where } \quad \mu_i = \beta_0+\beta_1 X_i }} $$ and from this we got that the conditional likelihood is $$ \boxed{ l(\beta_0,\beta_1,\sigma) \quad =\quad \displaystyle{-n \log(\sigma) -\frac{1}{2 \sigma^2} \sum_{i=1}^n\left(Y_i-\mu_i\right)^2 } } $$

If we in this case denote $L(a,b) = (a-b)^2$ then we can now phrase the linear regression problem as $$ \arg\min_{h \in \mathcal{H}} \sum_{i=1}^m L(h(x^{(i)}),y^{(i)}) $$

Note the shift in notation and how we deal with random versus observed. In the machine learning community they often work with "observed values" and just plug in the values. But the idea from which all of this originates and if one wants to make statistical machine learning rigorous, we need to use our terminology with random variables and consider "data" as being a set of random variables formally made precise by an underlying probability triple.

The Portland house price example using Sci-kit learn

In order to use sci-kit learns framework to "train" a linear regression model we will first have to prepare the data in the way that it expects. The format is as follows

Let's note the shapes of X and Y now.

This now gives us a fitted model for this particular data, so lets plot it.

Ofcourse we could use all available features to make multiple linear regression as follows

As we can see here, since the x-axis is size and the y axis is price we have an underlying variable which is number of bedrooms the line is not straight.

Let's also plot the number of bedrooms x[1] against the price (y-axis) next to appreciate the other discrete feature.

But remember, this is a linear model so if we consider the full 3-d space the predictions would be on a plane instead of a line.

Other models

Now that we have seen linear regression being viewed as a machine learning model through the concept of MLE, we can actually derive most other models that are being used in the machine learning world, but in order to describe the next model, let us first consider another example problem. It is the classical wine quality dataset.

This dataset is actually built into sklearn and we can load it as follows

Wine recognition dataset

Data Set Characteristics:

Number of Instances

178 (50 in each of three classes)

Number of Attributes

13 numeric, predictive attributes and the class

Attribute Information

  • Alcohol

  • Malic acid

  • Ash

  • Alcalinity of ash

  • Magnesium

  • Total phenols

  • Flavanoids

  • Nonflavanoid phenols

  • Proanthocyanins

  • Color intensity

  • Hue

  • OD280/OD315 of diluted wines

  • Proline

    • </ul> </dd> </dl>

    • class:

      • class_0

      • class_1

      • class_2