Earthquakes¶
Here is an extract from https://en.wikipedia.org/wiki/Earthquake:
An earthquake (also known as a quake, tremor or temblor) is the shaking of the surface of the Earth resulting from a sudden release of energy in the Earth's lithosphere that creates seismic waves. Earthquakes can range in size from those that are so weak that they cannot be felt to those violent enough to propel objects and people into the air, and wreak destruction across entire cities. The seismicity, or seismic activity, of an area is the frequency, type, and size of earthquakes experienced over a period of time. The word tremor is also used for non-earthquake seismic rumbling.
At the Earth's surface, earthquakes manifest themselves by shaking and displacing or disrupting the ground. When the epicenter of a large earthquake is located offshore, the seabed may be displaced sufficiently to cause a tsunami. Earthquakes can also trigger landslides and, occasionally, volcanic activity.
In its most general sense, the word earthquake is used to describe any seismic event—whether natural or caused by humans—that generates seismic waves. Earthquakes are caused mostly by rupture of geological faults but also by other events such as volcanic activity, landslides, mine blasts, and nuclear tests. An earthquake's point of initial rupture is called its hypocenter or focus. The epicenter is the point at ground level directly above the hypocenter.
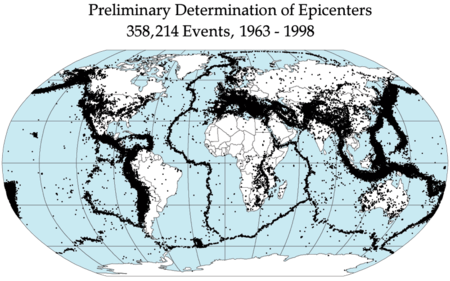
Having gotten some basic background on earthquakes (Seismologists are the domain experts of seismology or the study of earthquakes) as we will be analysing data fetched from New Zealand which is in the Ring of Fire along with Japan, Western American continental coastlines all the way down to Chile as rendered below.

Here are typical epicentres all across the globe.